朋辈辅导师第十二周直播课-矩阵相关典型问题的备课资料,大家有需要自取,备课本有点乱,建议配合视频一起食用。
资料在这->矩阵相关典型问题
有效期限:2025-11-11 23:59
分割线,下面是备课本
矩阵相关问题
[toc]
矩阵的基本盘
可逆定义定义及相关性质及求逆阵的方法
- 可逆的定义及相关性质
$若\exists B,AB=BA=I,则称A为可逆阵,B为A的逆阵,记作:A^{-1} = B $
- 性质:
$(ABC)^{-1} = C^{-1}B^{-1}A^{-1} $(proof)
行列式不为零则可逆
…… 逆阵唯一性
拓展唯一性例题的解法


保可逆,反序可逆
A可逆,B可逆,则AB可逆
$proof: ABB^{-1}A^{-1} = I $
若AB = I ,BA也可逆。- 求逆方法有三:增广,伴随,0化式(看见多项式赢麻啦)
增广矩阵的机理
伴随公式的引申
0化式,关于矩阵的多项式,例题,关于特征多项式(Caley定理)
正交及相关性质
$A^TA = I,即A^{-1} = A^T,则称A为正交阵 $
性质:矩阵乘的转置,与矩阵乘的求逆类似
- 保长、保内积、保正交
$我们知道向量的模长度公式是吧,对于列向量X,它的模长为||X||^2 = X^TX(内积的表示) ,所以列向量AX(A为正交阵)为||AX||^2 = X^TA^TAX ——保长性$
$保内积类似,(X,Y) = (AX,AY) = X^TY $
$保正交:两种理解:
A正交,B正交,则AB正交
X \perp Y \Leftrightarrow AX \perp AY $ - 线性变换初步
线性变换与内积空间来理解, Gram阵
- 每列为单位向量且相互正交,且则阵正交
用矩阵乘法去理解。
矩阵的秩
秩的xdm
- 阶梯阵概念,及其与向量组秩的联系。
矩阵就是向量组拼起来的,所以矩阵的秩就是向量组的秩。
我们在线性方程组的矩阵消元法中见识过,我们把一个矩阵变成阶梯状,我们考虑一下,变成阶梯状以后,后面的向量前缀都是零,所以不可能可以表示前面的向量,所以很简单,阶梯有多少阶,就会有多少秩。
那么到底是行向量的秩还是列向量的秩呢,不用纠结我们通过阶梯可以看出,行向量的秩就是列向量的秩。
所以三种同解变形,其实就代表着三种初等变换。 - 秩一阵
我们来看一个矩阵,秩一阵,可分解为两个向量之间的乘积。
我们在最后再来谈秩的各种公式的关系
- 满秩则有唯一解
$proof: \because r(A) = n $
$\therefore \{\alpha_1,……,\alpha_n\}可作为一组基 $
$\therefore \forall \beta \in R^n 都会存在\beta 的坐标(x_1,……,x_n) $
$坐标即为唯一解 $ - 满秩则可逆
$proof: 由上可知:AX_1 = \varepsilon_1, AX_2 = \varepsilon_2,……,AX_n = \varepsilon_n 都有解$
$所以AA^{-1} = I可解出A^{-1} = (X_1,X_2,……,X_n) $
- 满秩则有唯一解
所以说到这就只需要明确一个事情,满秩,行向量组列向量组无关,行列式不等于0,可逆,只有唯一解,非奇异这都是等价的概念
各种各样的秩公式
分块秩公式

积阵秩公式
- 乘积不增秩公式

- 积0公式

- 转置积秩公式

加减秩公式

奇妙的秩一阵
- 用一个例题来说明
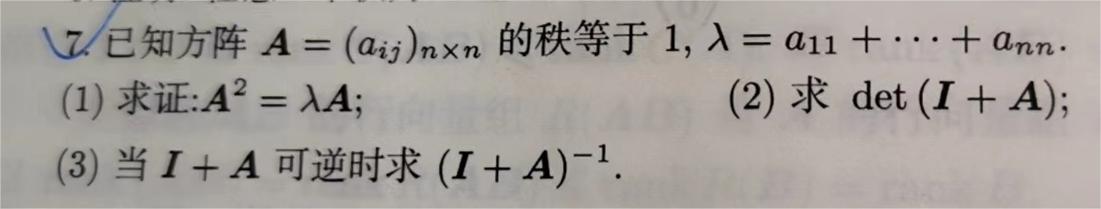
提一嘴先不讲
- 秩一阵的特征值
- 秩一阵+平移公式+特征值与行列式的关系
下降公式

换位公式1.0

换位公式2.0

换位公式3.0及特征值(带拓展,看时间)

奇妙的伴随阵
- 伴随阵的定义
- 伴随公式的推导

相关行列式值的推导
- 相关行列式的值的计算
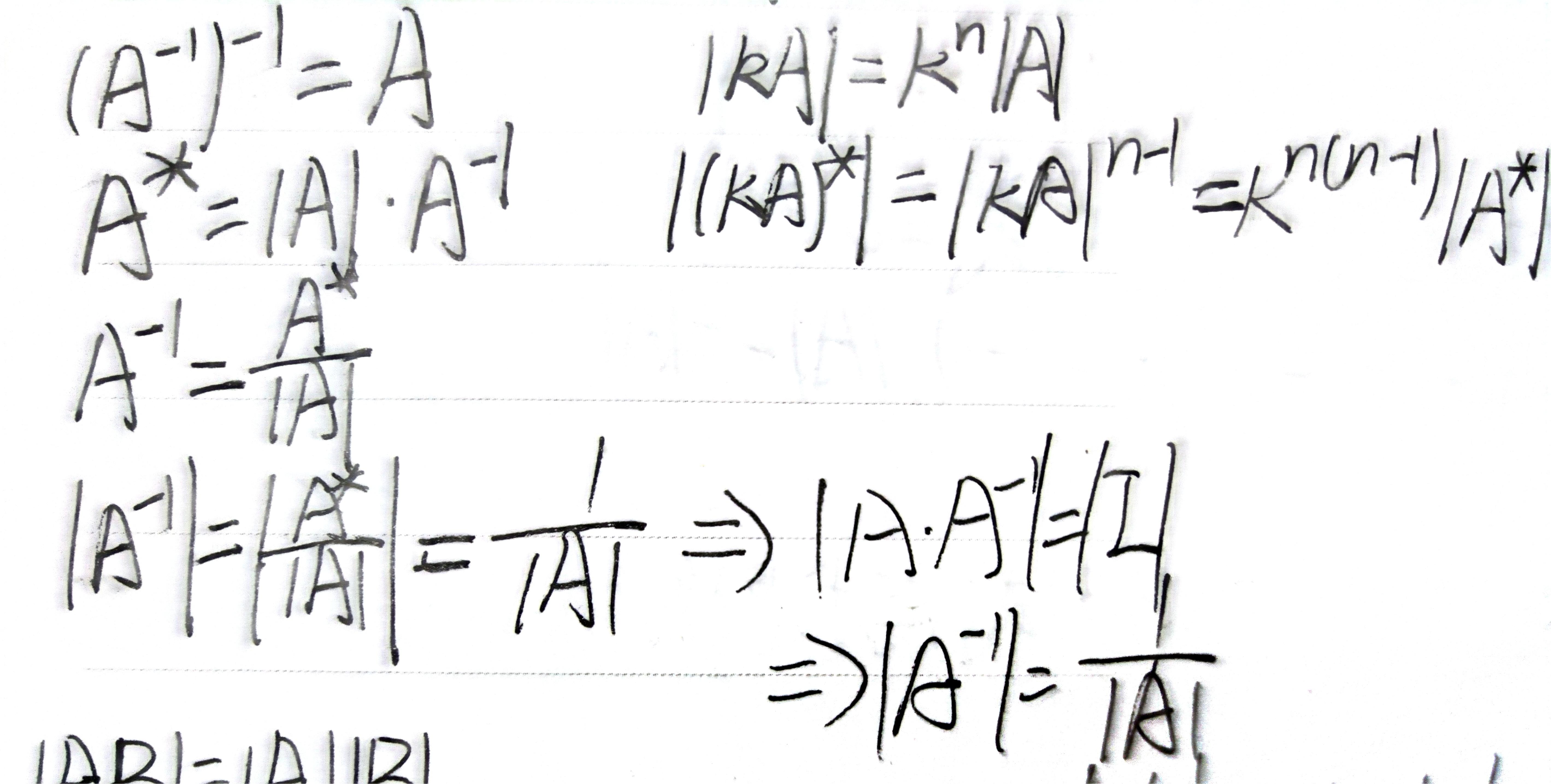
相伴秩公式
- 古典秩定义



