系边上老师的课边做的一些笔记以及自己的一些想法,但有时候可能会拖更,分享给大家,有不妥之处,敬请评论区指正。
热力学总结
内能、功、热量、热一律
- 系统的状态发生变化 -> 热力学过程
- 弛豫时间:系统由非平衡态达到平衡态所需的时间
- 准静态过程(平衡过程):过程无限(理想过程)缓慢,每个中间过程都无限接近平衡态(每一点都满足 $ PV = \nu RT$),可以用P-V图表示。
- 做功(机械能转化的量度):在准静态过程中:
$状态从 (P_1,v_1,T_1)到(P_2,V_2,T_2)$
$ A = \int _{1 \rightarrow 2} \vec{F} \cdot d \vec{l} $
$ = \int_{1 \rightarrow 2} P \cdot S \cdot dl = \int _{v_1} ^{v_2} P dV $- 在P-V图上体现为始末状态所围的面积
- $ \Delta V > 0 气体对外界做正功 ,在P-V图上,顺时钟循环 A > 0 $
- 热量也是一种能量交换的度量!
- 热力学第一定律:
$ 系统内能的增量:\Delta E = A’ + Q (A’ 为外界对系统做的功,Q为外界向系统传递的热量) $
$\therefore 外界对系统传递的热量 Q = \Delta E + A$
$ Q = dE + A$
气体的摩尔热容量
- $热容C:C = \lim _{ \Delta T \to 0 } \frac{ \Delta Q }{ \Delta T} = \frac{dQ}{dT} $
- $比热容:单位质量物质的热容 C_b = \frac{dQ}{mdT} : J/Kg \cdot K$
- $ 摩尔热容:J / mol \cdot K$
- 定容摩尔热容:
$ C_{V,m} = \frac{ (dQ)_V }{ \nu dT } = \frac{dE}{dT}+ P\frac{dV}{dT} \stackrel{dV=0}{=} \frac{dE}{dT} = \frac{i}{2}R $
- 定压摩尔热容:
$ C_{P,m} = \frac{dE}{dT}+ P\frac{dV}{dT} = \frac{i}{2}R+ P\frac{dV}{dT} \stackrel{PV=RT}{==} (\frac{i}{2}+1)R $
- 比热容比(泊松比):定压摩尔热容比定容摩尔热容
- 准静态过程的热量的计算
等值过程的过程方程和能量关系
我们研究一个过程可以着重研究四个方面:其特点、过程方程、过程曲线、能量关系。
- 等压过程
$ P=const, \frac{V}{T}=const$
$ A = \int _{V_1}^{V_2} P dV = \nu R \Delta T $
$ \Delta E = \nu \frac{i}{2} R \Delta T = Q_P - A $
$ Q_P = \nu C_{P,m} (T_2-T_1) $ - 等容过程
$ A = 0 (dV = 0) $
$ \Delta E = \nu \frac{i}{2} R \Delta T $
$ Q_V = \Delta E = \nu C_{V,m} \Delta T = \frac{i}{2} V \Delta P $ - 等温过程
$PV = const, \Delta E = 0 $
$Q_T = \nu C_{T,m} \Delta T $
$\because \Delta T = 0,Q_T为有限量 \Rightarrow C_{T,m} = +\infty $
$Q_T = A = \int _{1 \to 2} PdV = \int_{V_1}^{V_2} \nu \frac{R}{V}TdV $
$=\nu R T \ln{\frac{V_2}{V_1} } = \nu R T \ln{\frac{P_1}{P_2} } $
绝热过程
- 绝热过程:系统在整个过程中,始终不和外界交换热量。
$ 特点:dQ = 0 , C_{Q,m} = 0 $
$ dQ = 0 \Rightarrow dA + dE = 0 $
$ 我们利用等容关系能得到:-PdV = \nu C_{V,m} dT $
$ 但是我们在绝热过程中P,V都会变$
$ \therefore 对克拉伯龙方程微分 $
$ PdV+ VdP = \nu R dT $
$ 把上式代入得:(C_{V,m}+ R)PdV = - C_{V,m} V dP $
$\therefore \frac{dP}{P} = - \gamma \frac{dV}{V} $
$ 两边求导:PV^{\gamma} = const (过程/泊松方程) $ 绝热曲线:
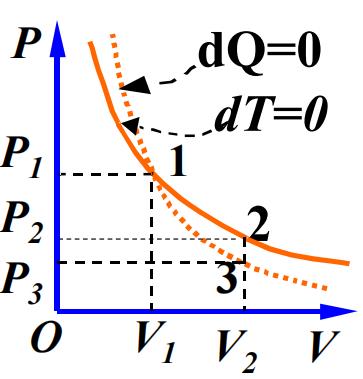
- 我们来仔细辨析一下其中的原理,从宏观和微观的角度。
能量关系:
$ \Delta E = \nu \frac{i}{2} R \Delta T = \nu C_{V,m} \Delta T = -A$
$\because \frac{i}{2} = \frac{1}{\gamma - 1} $
$\therefore A = \frac{P_1 V_1 - P_2 V_2}{ \gamma - 1} $- 当然,我们也可以通过理气对外做功的方程以及泊松方程直接求A
$A = \int_{V_2}^{V_1} PdV = $
- 当然,我们也可以通过理气对外做功的方程以及泊松方程直接求A
多方过程
- 多方过程:理想气体的一般过程。
- $ 过程方程:PV^n = const $
- 从方程可以看出,这个过程介于等压过程和等容过程之间,为啥这么说捏?
- 从方程可以看出,这个过程介于等压过程和等容过程之间,为啥这么说捏?
循环过程
- 循环过程:从初始状态出发,一系列变化回到初始状态
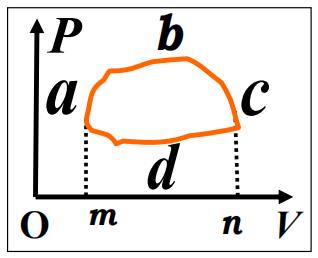
- $特点:\Delta E = 0 \therefore A = Q $
$A = \int_LPdV = \pm S_{abcda} $
$ A的\pm 取决于L路径的正负$ - 应用:热机与制冷机
拓展—热力经济学
持续更新中。。。


